我们已经接触了很多对于数组排序的算法，比如冒泡排序、选择排序、快速排序、插入排序、希尔排序、归并排序等，算法这么多，我们到底该在实际运用中选择哪一个呢？这就涉及到了取舍的问题，当然我们取舍的重点是算法的运行效率。那算法的运行效率到底如何评价呢？有的人说，你写一个测试程序运行一下（事后统计法），看看具体使用了多少时间不就知道了吗？当然这是一种办法，但是它还有很多的缺陷，下面我们就详细介绍一下算法统计的两种方法，一种称为“事后统计法”，另外一种称为“事前分析估算”。
【事后统计法】
统计方法：
- 比较不同算法同一组输入数据的运行处理时间。
缺陷：
- 为了获得不同算法的运行时间必须编写相应的测试程序。
- 运行时间严重依赖硬件及运行时间的环境因素。
- 算法的测试数据的选取相当困难。
总结：
- 时候统计法虽然直观，但是实际困难且缺陷多。
【事前分析估算】
统计方法：
- 依据统计的方法对算法效率进行估算
影响算法效率的主要原因：
- 算法采用的策略和方法
- 问题的输入规模
- 编译器所产生的代码
- 计算机执行速度
算法推倒的理论基础：
- 算法最终编译成具体的计算机指令
- 每一个指令，在具体的计算机上运行速度固定
- 通过具体的步骤，就可以推导出算法的复杂度（如下图）
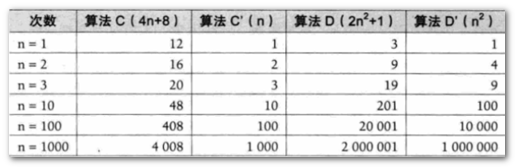
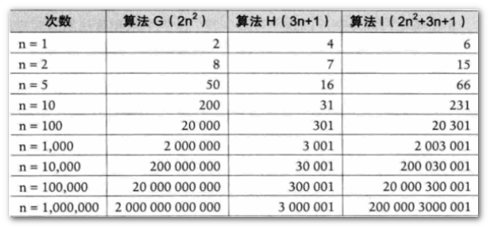图中我们可以看出，随着n值的增加，每种算法最终的数据会越来越大，这个数据就代表了算法的执行次数，既然执行速度是固定的（第二条规则），那么次数越多随之时间也就用的越多，这就是算法的复杂度。 怎么判断一个算法的效率？（规则如下）：
- 判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略。
- 在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度。
- 只有常数项记做1
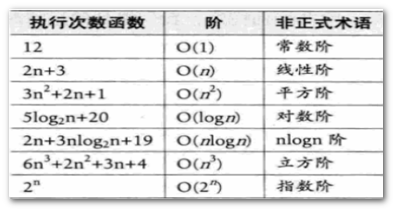
用什么标志来表示算法的效率？
- 大O表示法，如下常见的时间复杂度：
常见时间复杂度之间的关系图：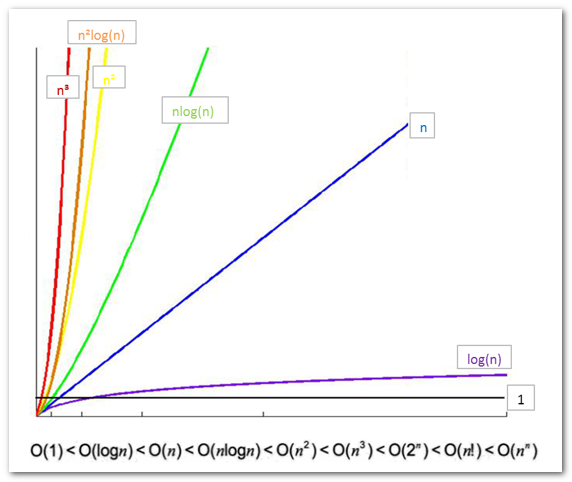 
上图就是不同的时间复杂度所用的时间表示图。如果是O(1)用的时间最短、其次是O(logn)，一次类推。 时间复杂度的小练习（参考算法的效率规则判断） O(5) = O(1) O(2n + 1) = O(n) O(n2 + n + 1) = O(n2) O(3n3 + 1) = O(n3) 总结：只关注最高次项、时间复杂度是指最坏的时间复杂度、只有常数项记做1
【算法的空间复杂度】
计算方式：
- 通过计算算法的存储空间实现
公式：
- S(n) = O(f(n))
- n为问题规模，f(n))为在问题规模为n时所占用存储空间的函数
- 当算法执行时所需要的空间是常数时，空间复杂度为O(1)
空间与时间的策略：
- 多数情况下，算法执行时所用的时间更令人关注
- 如果有必要，可以通过增加空间复杂度来降低时间复杂度
- 同理，也可以通过增加时间复杂度来降低空间复杂度
练习：
- O(4n+12) = O(n)
- O(8) = O(1)
- O(4) = O(1)
总结：实现算法时，需要分析具体问题，对执行时间和空间的要求。
【结合代码综合练习】
long sum1(int n)
{
long ret = 0;// 时间只走了一步 1 // 空间 long 占 4 个字节，就是 4
int* arr = (int*)malloc(n * sizeof(int));// 时间只走了一步 1 // 空间int4个字节，就是 4 * n
int i = 0;// 时间只走了一步 1 // 空间 int 占 4 个字节，就是 4
for (i = 0; i < n; i++)// n无法确定就是n步 n // 空间没有分配 是0
{
arr[i] = i + 1;
}
for (i = 0; i < n; i++) // n无法确定就是n步 n // 空间没有分配 是0
{
ret += arr[i];
}
free(arr);// 只走了一步 1 // 空间没有分配 是0
return ret;// 只走了一步 1 // 空间没有分配 是0
}
// 从上面的例子可以看出，时间复杂度是两个n加上5步普通语句，就是 2n + 5，换算成大O表示法就是 O(n)
// 空间复杂度，分配存储空间的是 4 * n 的大小，再算上第一句和第三句，那最终结果是 4n + 4 + 4 == 4n + 8，换算成大O表示法就是 O(n)
上面计算了一个简单的从1加到100的一个算法的复杂度。下面我们来看看冒泡排序的时间复杂度：
void popSort(int arr[], int len)
{
// 两次for循环，循环了len次，相当于 n*2，其他单步步骤不及
// 最终转换为大O表示法就是 O(n^2)
for (int i = 0; i < len - 1; i++)
{
for (int j = 0; j < len - i - 1; j++)
{
if (arr[j] > arr[j + 1])
{
arr[j] = arr[j] ^ arr[j + 1];
arr[j + 1] = arr[j] ^ arr[j + 1];
arr[j] = arr[j] ^ arr[j + 1];
}
}
}
}